Laser generated plasma is an area which is currently receiving much attention due to rapid advances in laser technology. From a theoretical point of view these are particularly interesting, as laser pulses generally deliver highly localized, strong electric and magnetic fields with short temporal duration. This leads to extremely non-thermal electron and ion distributions, and a large number of instabilities in the plasma and involving the laser. Non-thermal distributions are not limited to laser plasma scenarios however, but appear in fusion plasmas such as in tokamaks, food processing and astrophysical situations, to name a few. A non-thermal distribution means that a kinetic description is required, where the velocity distribution of particles is not averaged as in a fluid model. An additional problem that arises in laser plasma interactions is that often the interaction is with high-density plasma, such as in an interaction with a solid target. The localization of the heating means that there are areas of colder, denser plasma for which collisions are not negligible.
Formulation of models that can properly and accurately describe electron transport and magnetic field generation under realistic laser–plasma conditions is a challenging task. There are a number of established processes for modeling kinetic effects in plasma. In particular, the particle-in-cell method is a very well established technique that models the particles as a number of larger `macroparticles’ each representing a large number of the fundamental particles. These are then temporally evolved by solving the Newton-Lorentz force law for each macroparticle. These have a finite size to reduce short-range interactions that would be unphysically significant otherwise. Although highly successful as a technique, the lack of collisional effects in the basic model and the large number of particles required to accurately model effects due to the shape of the distribution are limitations.
PIC Simulation
The physics of interaction of the intense laser pulse with plasma is very complex. It is common to use Particle-In- Cell (PIC) simulations, which track the motion of individual plasma particles (electron and ions) in surrounding electrostatic and magnetic fields. These simulations are typically very intense and time consuming, and are generally performed on computers with massively parallel processing capabilities. To study in detail the features of laser-plasma interaction observed in a laser wakefield acceleration experiment we performed 3D PIC simulations for the parameters close to the experimental conditions using the OSIRIS 2.0 framework [1]. These show the evolution of the laser pulse in plasma, electron injection, and the characteristics of electron acceleration observed in experiments.
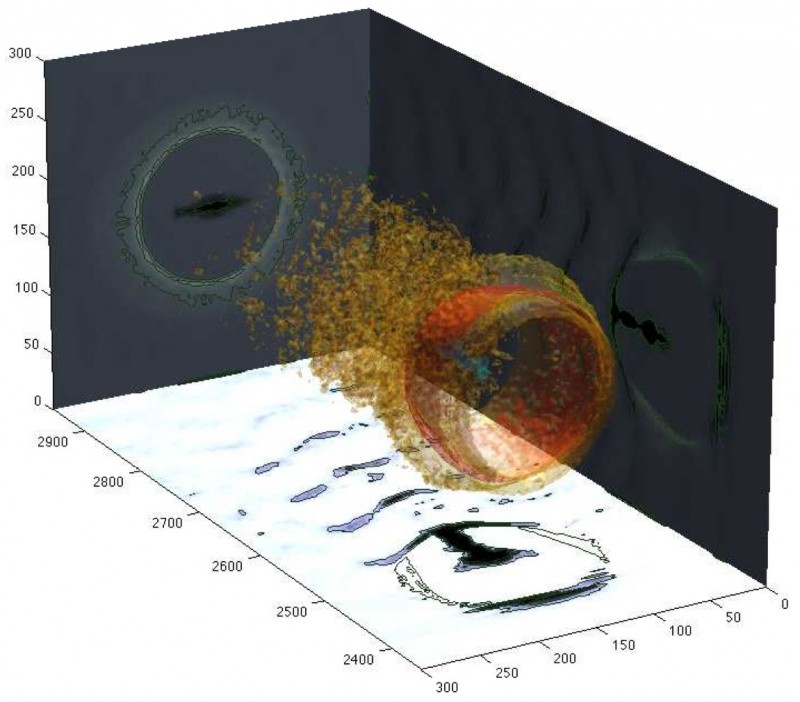
Fig. 2. The bubble formed in the wake of the HERCULES pulse, according to a 3D Particle-In-Cell simulation using the OSIRIS 2.0 framework [1].
Fig. 2 shows a snapshot of electron density from PIC simulations after the pulse has propagated about 100 microns in plasma. In this picture darker colors correspond to higher electron densities and the lighter ones to lower densities. One can see that plasma electrons are expelled from the axis by the relativistically intense laser pulse and form a bubble-like structure (or bare ion cavity) behind the pulse, with a longitudinal dimension close to the plasma wavelength, and a transverse dimension close to the laser focal spot size. This bubble is essentially devoid of electrons and moves through the background ion plasma with a speed close to the speed of light. Some of the background electrons streaming around the plasma bubble are pulled back to the laser axis behind the cavity. These electrons may be trapped and accumulated inside the bubble. They constantly gain momentum by propagating through the plasma and reach high energies in a monoenergetic electron bunch.
Radiation Production
We have developed an algorithm which uses a combination of numerical and analytic methods to integrate the Lienard-Wiechert fields, for arbitrary trajectories of many charged particles, to frequencies greatly exceeding the Nyquist frequency [2]. This means that the sampling rate to accurately reproduce a particular spectrum can be many orders of magnitude lower than the inverse of the Nyquist frequency and therefore faster to solve numerically. This algorithm is particularly relevant to calculations of radiation from betatron oscillations in laser wakefield accelerators and beam-laser interactions such as non-linear Thomson scattering , but the technique is applicable to numerous other areas of physics.
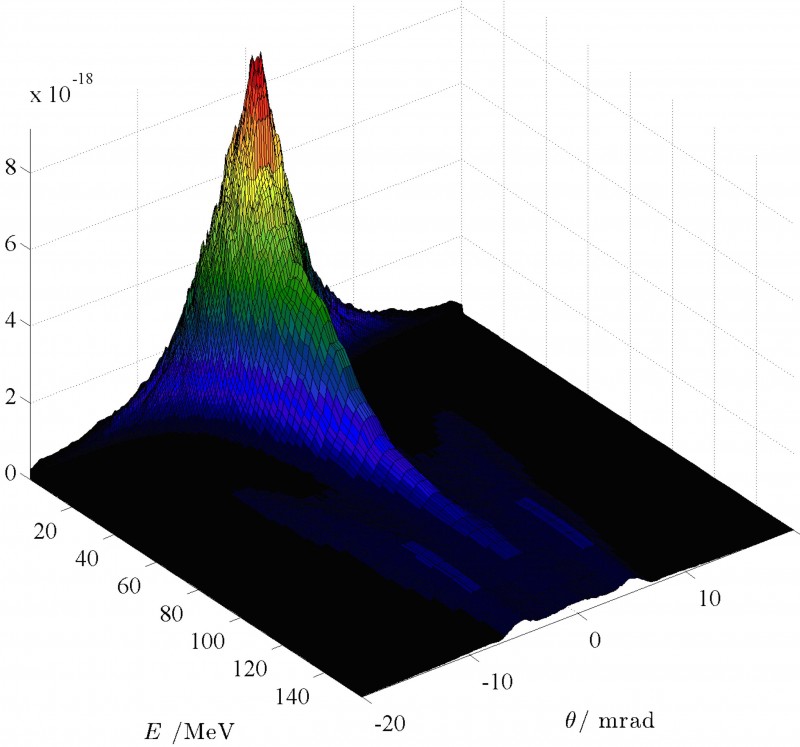
Fig.1. The angularly resolved spectrum calculated for a 150 MeV beam colliding with the tightly focused HERCULES pulse.
This technique has been coded into a particle tracking code using a 4th order Runge-Kutta integration of the covariant equation of motion including radiation reaction forces, known as Radampeltrac. Using this code we have recently demonstrated the effect of the interaction between laser field and electron beam on the spectrum of photons radiated from a plasma bubble [3] and has also been used in confirming an analytic formulation of the radiation spectrum from a plasma bubble [4].
Vlasov-Fokker-Planck simulation
The Vlasov-Fokker-Planck (VFP) equation is a conservation equation in 6D phase-space, with a smooth electron distribution function f representing a statistical average of the particles within a differential volume element. It includes the effect of both the conservation of f in the presence of macroscopic electric, E, and magnetic, B, fields, and the small angle Coulomb deflections of the underlying inter-particle interactions.
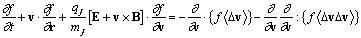
IMPACTA solves the cartesian expanded Vlasov-Fokker-Planck equation for the electrons using an implicit scheme, with non-linear terms treated by iteration of the matrix solution. The algorithm used for solving the matrix equation is a routine from the Portable, Extensible Toolkit for Scientific Computation (PETSc). Expansion of the distribution, which in IMPACT [5] is truncated after first order, has been extended to include second order (f2) terms. The code uses a two dimensional cartesian spatial geometry for the spatial grid. This is particularly relevant to magnetized plasma.

Fig. 3. Magnetic fields generated by an anisotropic electron distribution in a ns high energy laser-plasma interaction [7].
The code uses an implicit finite difference algorithm to solve the components of the expanded Vlasov-Fokker-Planck equation, in addition to the Faraday and the Ampère-Maxwell equations for the fields. IMPACTA currently uses the Lorentz approximation (valid for high Z), whereby electron-electron (e-e) collisions are neglected in the equation for f1. The term for electron-ion (e-i) scattering is retained in all equations in the reduced form where it is ∝ 1/v3 . The neutralizing ion background is now mobile, via the hydrodynamic model used in [6], but including the effect of the full pressure tensor in updating the ion velocity. The inverse bremsstrahlung model has been extended to include f2 effects, and a Weibel damping term has also been optionally included. Absorption of laser energy is modeled using the extended version of Langdon’s operator.
The codes IMPACTA and Radampeltrac were developed by members of the Center for Ultrafast Optical Science. The OSIRIS 2.0 framework for PIC simulation is developed and maintained by UCLA/USC/IST Portugal.
1. R. Fonseca et al., Lecture Notes in Computer Science (2002).
2. A. G. R. Thomas, Phys. Rev. ST-AB (2010).
3. A. G. R. Thomas and K. Krushelnick, Phys. Plasmas (209).
4. A. G. R. Thomas, Phys. Phys. Plasmas (2010).
5. R. J. Kingham and A. R. Bell, J. Comp. Phys. (2004).
6. C. P. Ridgers, R. J. Kingham and A. G. R. Thomas, Phys. Rev. Lett. (2008).
7. A. G. R. Thomas, R. J. Kingham and C. P. Ridgers, New J. Phys. (2009).
