Accelerating electrons to relativistic energies can be an expensive business – the next generation of particle accelerators will be many kilometers in size and are likely to cost billions of dollars. However, one of the potential ways to reduce the size and cost of future accelerators for use in both fundamental physics experiments and technological applications is to utilize the huge (hundreds of GigaVolts per meter) electric fields in laser-produced plasmas to accelerate electrons. These fields are thousands of times greater than the accelerating fields in conventional accelerators. In the laser-produced plasma electrons can pick up energy from the waves in plasma just as a surfer picks up energy from an ocean wave. These waves are generated when an intense laser pulse propagates through the plasma and displaces background electrons through the ponderomotive force (or light pressure) of the laser [1]. These waves propagate near light speed behind the laser pulse. For sufficiently large amplitude plasma waves, electrons in the background plasma can be trapped and accelerated by the longitudinal electric fields of the waves to very high energies over very short distances. Fig. 1 demonstrates principle of laser wakefield electron acceleration.
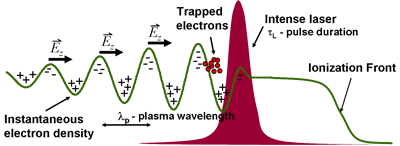
Fig. 1: Schematic of the intense laser pulse interaction with the initially neutral, low atomic number gas (i.e. Hydrogen or Helium). Gas is ionized with the foot of the pulse and the wakefield is created behind the laser. Trapped electrons in the right phase can be accelerated to very high energies. The plasma wave is excited most efficiently when the plasma wavelength is equal to the laser pulse duration.
CUOS researchers were among the first to observe beam of energetic electrons from the laser wakefield with longer laser pulses (~1 ps) [2,3]. These high-energy electrons had the Maxwellian spectrum. In a past few years significant progress was made towards improving the quality of the electron beam. A research group of Karl Krushelnick back at the Imperial College (UK), the groups at LOA (France) and Berkley (US) using sub-100 fs laser produced “monoenergetic” beams of relativistic electrons [4-6] (see Fig. 2) with energy 60-170 MeV.
Fig. 2: Relativistic plasma effects: a laser-generated wake field produces high quality relativistic electron beams (cover of Nature 431 (2004)).
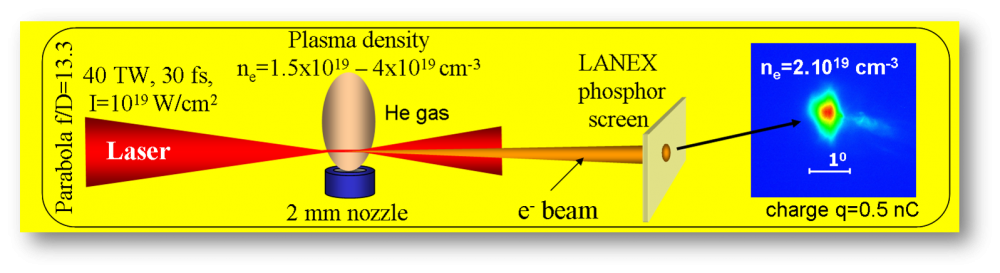
At CUOS using a 30 fs, 40 TW Ti:sapphire Hercules laser focused to the intensity of 10^(19) W/cm^2 onto a supersonic 2 millimeter He gas jet, we observed quasi-monoenergetic electron beams with energy up to 300 MeV and an angular divergence of 10 mrad [7,8]. The schematic of the experiment is presented in Fig. 3.
Fig. 3: Experimental setup of the laser wakefield electron acceleration from gas jet target. On the right – picture of the electron beam with divergence of 0.5 degree (FWHM) detected using LANEX phosphor screen and CCD.
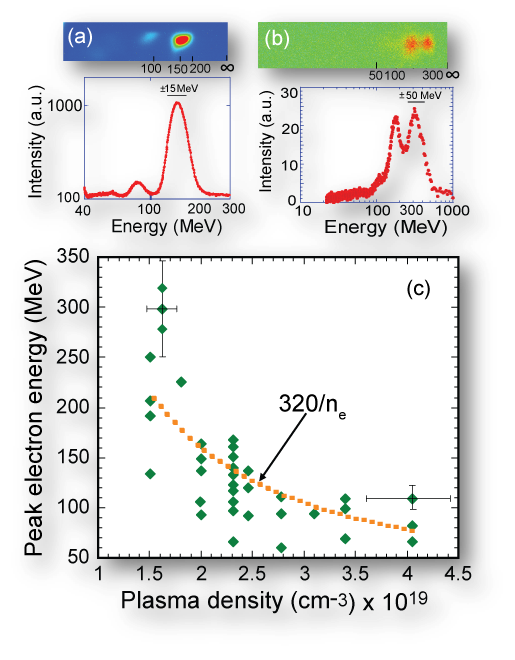
In these experiments we demonstrated that the energy, charge, divergence and pointing stability of the beam can be controlled by changing the plasma electron density and that higher electron energies and more stable beams are produced for lower densities (Fig. 4). The characteristic scaling of the electron beam energy was consistent with dephasing of the electrons from the plasma wave (Fig. 4c). High-energy electrons propagating in a dense plasma with a length greater than the dephasing length may lose their energy by outrunning the plasma wave and by going into the deceleration phase.
Fig. 4: Measured electron spectrum and lineout for plasma density (a) n_e=2.5×1019 cm–3 with maximum energy of 145 MeV, and (b) ne=1.5×1019 cm-3 exhibiting a double peak structure with maximum energy of 320 MeV. (c) The dependence of the maximum electron energy versus plasma density. Dotted line is a power fit.
The physics of interaction of the intense laser pulse with plasma is very complex. It is common to use Particle In Cell (PIC) simulations, which track motion of individual plasma particles (electron and ions) in surrounding electrostatic and magnetic fields. These simulations are typically very intense and time consuming and performed on computers with massive parallel processing. To study in detail the features of laser-plasma interaction observed in the experiment we performed 2D PIC simulations for the parameters close to the experimental conditions which show the evolution of the laser pulse in plasma, electron injection, and the specifics of electron acceleration observed in experiments. Fig. 5 shows a snapshot of electron density from PIC simulations after the pulse has propagated about 800 microns in plasma. In this picture darker colors correspond to higher electron densities and the lighter ones to lower densities. One can see that plasma electrons are expelled from the axis by the relativistically intense laser pulse and form a bubble-like structure (or cavity) behind the pulse with a longitudinal dimension close to the plasma wavelength and a transverse dimension close to the laser focal spot. This bubble is a void of electrons and moves through the background ion plasma with a speed close to the speed of light. Some of the background electrons streaming around the “bubble” fall back to the laser axis behind the cavity. These electrons are captured and accumulated inside the bubble. They constantly gain momentum propagating through the plasma and reach high energies producing a monoenergetic electron bunch.
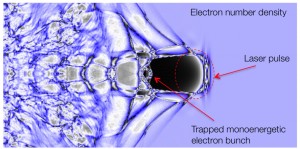
Fig. 5: Electron density distribution and generation of quasi-monoenergetic electron bunches observed in PIC simulations.
The generation of tunable monoenergetic electron beams with energies of 1 GeV and above, high bunch charge, stable and reproducible output characteristics from a single laser-wakefield stage will require guiding of sub-PW laser pulses in a preformed plasma channel or capillary discharge plasma, with properly chosen electron density, combined with an external electron injection. Such improved parameters of electron beams are necessary to make plasma-based accelerators a practical tool for high-energy physics and medical applications. Electron driven femtosecond x-ray generation would also be enhanced by such improvements providing new capabilities for basic studies in biology, solid state and plasma physics.
Frequency Domain Holography
Electron beam quality parameters from LWFAs such as energy, energy spread, angular divergence, bunch charge, and its duration depend sensitively on the plasma wakefield structures. Direct visualization of these structures and their evolution is critical for understanding and controlling LWFA output.
Together with Prof.Mike Downer’s group at the University of Texas we meet this challenge by recording two-dimensional features of the plasma wave in a single shot using frequency-domain holography (FDH). The holographic snapshots record multiple wake periods of the mildly non-linear non-broken plasma wake and capture the buildup of the wave front curvature with the distance behind the driver the features previously seen only in the simulations [11].
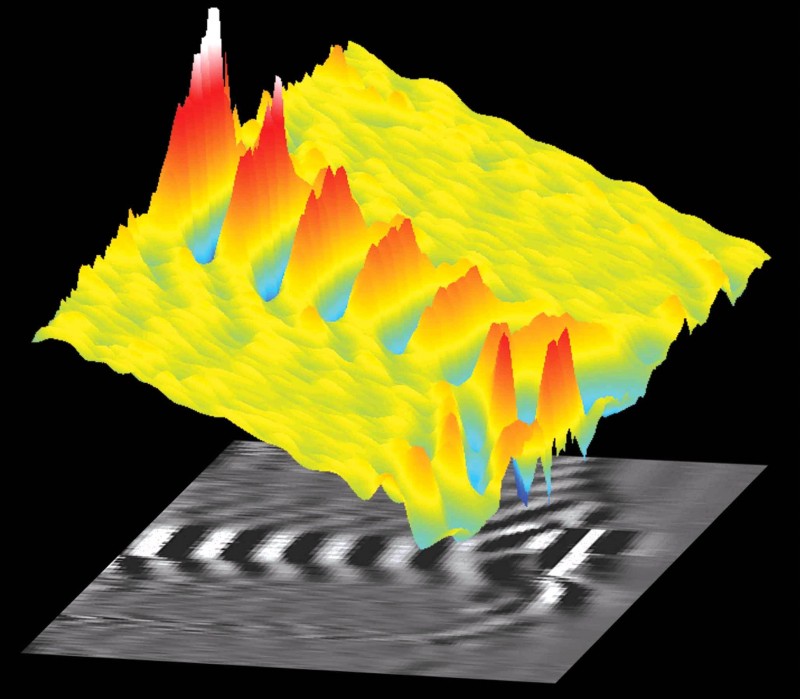
Fig. 6: Snapshot image of a plasma wakefield produced by the 30 TW HERCULES laser.
Ionization Trapping
In the strongly nonlinear regime, the laser pulse expels electrons from its focal volume but has a negligible effect on the remaining ions, resulting in a cavity with strong electromagnetic fields. Electrons from the periphery of the cavity are pulled inwards by the strong Coulomb attraction and form a thin high-density sheath around an approximately spherical `bubble’. This has ideal accelerating and focusing properties for electrons within the cavity, and at the point where the sheaths cross at the rear of the bubble, the field is particularly strong. Here, electrons can be accelerated to the phase velocity of the bubble in a time shorter than their crossing time and are therefore trapped. Under certain conditions, the trapped electron beam can have a quasi-monoenergetic energy distribution.
Control of the onset of this self-trapping is not independent of the accelerated electron beam charge, peak energy and emittance, as both depend on the drive laser pulse characteristics and global plasma density [Maksimchuk ApplPhysB (2007)]. Initiating trapping independently of the acceleration process can be performed by implementing an external injection source of electrons or using an additional laser pulse to cause injection [Umstadter PRL (1996)]. In that reference, the proposed mechanism was to use a second high intensity laser to field ionize electrons within the wake to initiate trapping. A related ionization trapping mechanism has been demonstrated in electron beam driven plasma wave accelerator experiments on the Stanford Linear Collider (SLAC) due to the electric field of the bunch.
The self-trapping condition is that an electron gains sufficient forward momentum from the longitudinal electric field to reach the phase velocity of the bubble before it slips out of the accelerating phase. Creation of free electrons by ionization, initially at rest within the electron cavity, can initiate trapping because these experience additional energy gain due to the net potential difference between the edge of the bubble and its interior. This translates to a lowered trapping threshold, and is maximized if they are initiated at the minima of the potential.
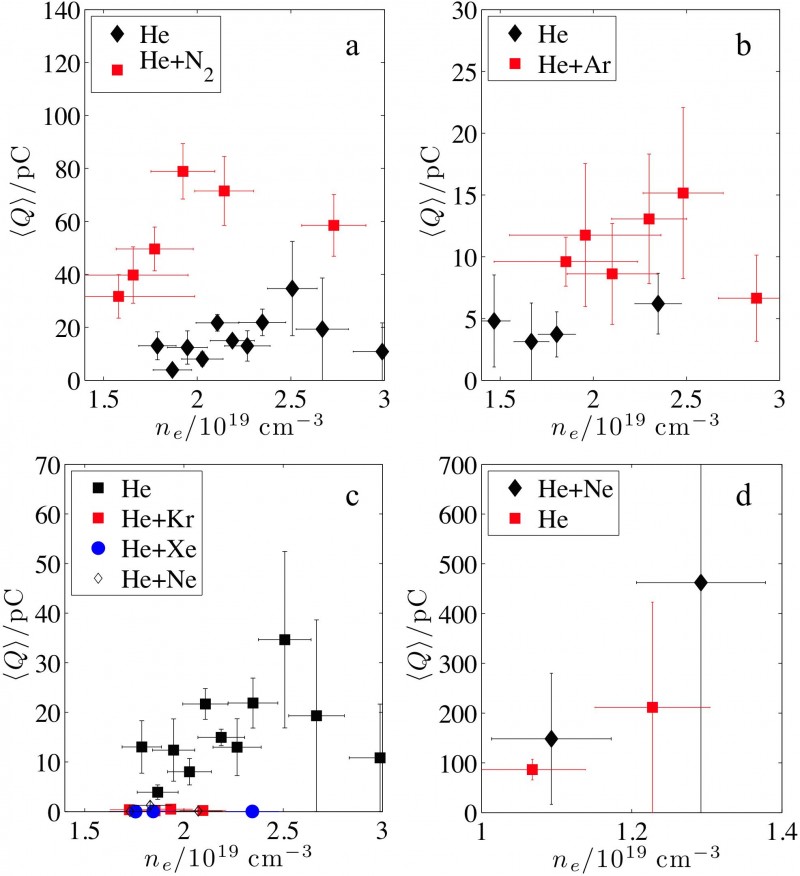
Fig.7. Integrated charge above 30~MeV measured by the electron spectrometer as a function of electron number density.The values represent an average of 5-20 shots for which electron signal is clearly above background. The experiments were performed with a laser power of (a) 30 TW, (b) 24 TW, (c) 30 TW and (d) 120 TW.
Stimulated Raman Scattering
Propagation of the ultra-short laser pulse in underdense plasma was studied in the parameter range relevant for the laser wakefield accelerators. The transverse interferograms obtained from the experiments shows stimulated side Raman scattering (SSRS) which is well correlated with filamentation of the laser pulse. Experimentally obtained scattered light angle from the laser axis is well reproduced by an analytic formula for SSRS in the range of the plasma density from the experiments. 2D particle-in-cell (PIC) simulations showed that laser beam evolution is dominated by SSRS.
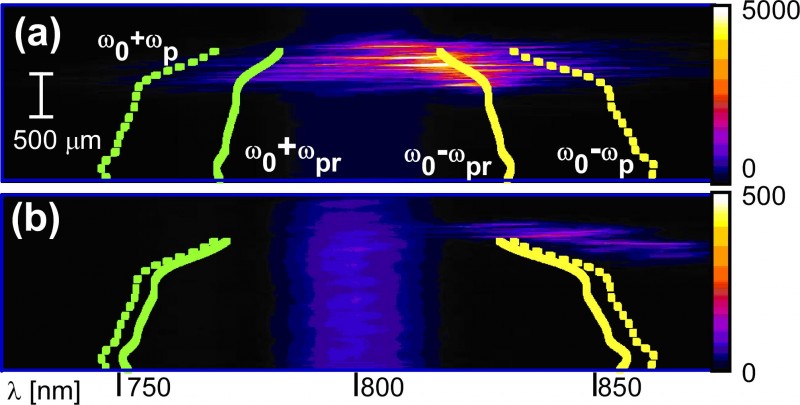
More info can be found in:
T. Matsuoka, C. McGuffey, P. G. Cummings, Y. Horovitz, F. Dollar, V. Chvykov, G. Kalintchenko, P. Rousseau, V. Yanovsky, S. S. Bulanov, A. G. R. Thomas, A. Maksimchuk, and K. Krushelnick, “Stimulated Raman side scattering in laser wakefield acceleration,” Phys. Rev. Lett. 105, 034801 (2010).
Photonuclear reactions with monoenergetic electron beams
Energetic electron beams produced by laser wakefield acceleration have an array of applications in radiography, radioisotope production, nuclear physics, and possibly the transmutation of nuclear waste. In particular, the multi-MeV bremsstrahlung produced using high-energy laser wakefield accelerated electrons incident upon a high Z converter is an effective technique to induce photonuclear reactions and photo-fission on a table-top [12,13] and may have additional applications in dynamic gamma-ray radiography and nuclear resonance fluorescence to detect explosives or other materials. Activation of nuclei by gamma-induced reactions requires gamma-ray energies corresponding to the giant dipole resonances of the nuclei, which typically lie in the 10-20 MeV energy range for (gamma, n) reactions and 5-10 MeV for (gamma, fission) reactions. Generation of gamma-rays lying within the giant resonance energy range can be made very efficiently with a high energy monoenergetic electron source. We optimized the electron beam’s spatial profile and its total charge, and consistently generated a quasi-monoenergetic electron beam with a peak energy ranging between 100 and 150 MeV by adjusting plasma background density. After characterizing the electron beam and establishing its reproducibility, a 2.9 mm thick, 11 mm diameter natural uranium target was placed 15 cm behind the gas jet, where the electron beam was approximately 3 mm in diameter. Bremsstrahlung yield scales as the atomic number squared Z2 thus the uranium target was used both as a converter and as a fissionable target (Fig. 9).
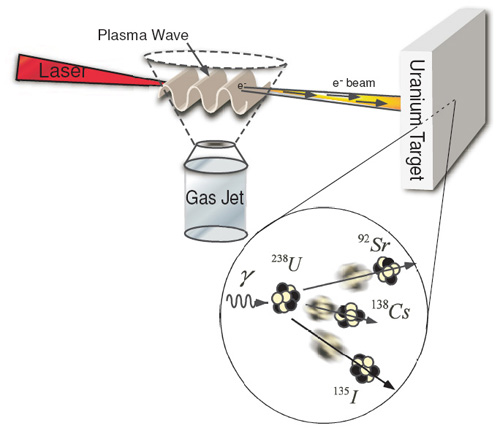
Fig. 9: Experimental setup for photo-fission using high-energy electrons from laser wakefield.
The uranium fission process produces, among other fission fragments, 134Iodine and 92Strontium with 53 min and 2.7 h half-lives, respectively. The laser was fired 72 times over 75 min, corresponding to roughly 1.5 134IodineI half-lives, and an additional 18 min delay was experienced between removing the sample and the counting process. The emitted gamma spectrum was recorded every 10 min for the first 1.5 h, every 20 min for the next hour, and finally every 60 min for the next 7 h. The 134Iodine and 92Strontium fission products were identified, using an ORTEC GAMMX Ge(Li) gamma-ray detector, through their signature gamma decays of 0.847 MeV and 1.384 MeV gamma rays (Figure 10).
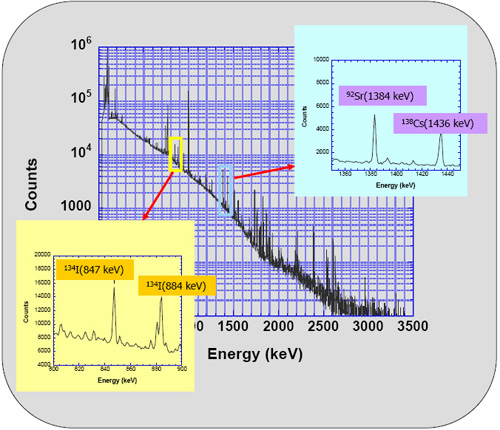
Fig. 10: The gamma spectra taken from the irradiated uranium target. The signature gamma-emission peaks from 134Iodine (847 keV) and 92Strontium (1384 keV) decay are shown.
The presence and populations of 134Iodine and 92Strontium were confirmed by measuring the numbers of the emitted gamma rays as functions of time, as shown in Fig. 11. Primary fission to the134Iodine fragment accounts for about one-third of the integrated total reactions. Feeding of the134Iodine population through the decays of other 238Uranium fission fragment pathways causes the deviation observed during the first 2 h of the measured 134Iodine decay. The secondary fission fragment pathways decaying to 92Strontium have shorter and decayed during the 18 min delay before counting began, thus showing little deviation from the single exponential decay model. By fitting the data after several expected lifetimes, 1.0 h and 2.64 h half-lives were determined for134Iodine and 92Strontium, respectively, in relatively good agreement with the literature values of 53 min and 2.7 h.
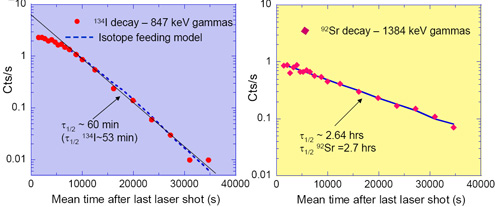
Fig. 11: Measured count rates for 847 keV and 1384 keV gamma rays detected, as a function of time after the last laser shot for 238U (gamma, fission) 134I and 238U (gamma, fission) 92Sr processes.
To derive the fission yields the tabulated lifetimes and relative fission fractions for fragments contributing to 134Iodine (and 92Strontium) were used. The apparent total 134Iodine and92Strontium isotope production yields after the last laser pulse derived from fitting the data with this model are 1.5×107 and 1.0×107, respectively. Dividing the totals by the appropriate effective number of laser shots, and taking into account the decays between shots, gives a resultant total average fission yield of 3.3×105 fissions per laser shot for both the 134Iodine and 92Strontium data sets, which is more than an order of magnitude greater than previously achieved.
Wakefield electron acceleration using the Lambda cubed laser
At CUOS, electron acceleration has been demonstrated in an unexplored regime of plasma wakefield driven by our high repetition rate (0.5 kHz) Lambda Cubed laser. The 30 fs, sub-TW laser is focused by an f/2 off-axis paraboloidal mirror onto the gas flow from a fused silica capillary tubing with an inner diameter of 100 microns. Stable collimated electron beams are produced with quasi-monoenergetic spectra up to approximately 150 keV. Using a low energy laser pulse (only 8 mJ available on target) to accelerate electrons requires a short under dense plasma, as laser depletion in generating the plasma wave limits the acceleration length. Electron trapping in the plasma wave is also difficult due to the lower achievable intensity. For our experiment parameters, simulations show that electron trapping occurs in an in homogeneous plasma from the density down ramp of a 100 microns scale gas target. The simulation results agree very well with the experiments. The high repetition rate capability enables better statistics and higher average particle flux, which were not accessible in previous experiments. It also allows “real time” optimization for electron beam profiles and electron energies. Because of the relatively high charge (~10 fC) and potentially short temporal duration, such electron sources have the potential to be used for ultrafast electron diffraction applications [14].
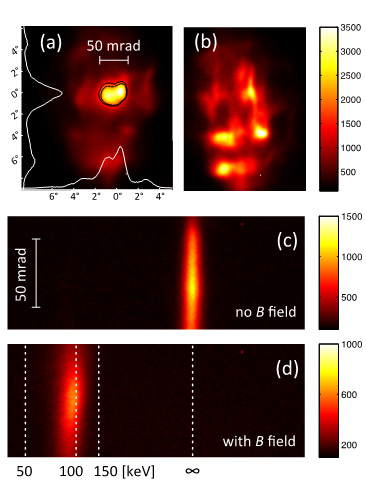
FIG. 12. (a)-(b): Images of electron beam profiles measured on Lanex screen (a) a typical collimated electron beam; (b) filamented electron beam. (c)-(d): Lanex images showing the electrons deflected by the insertable magnet spectrometer (c) without magnets (d) with magnets.
References
1. T. Tajima, J. M. Dawson “Laser-electron accelerator” Physical Review Letters43, 267 (1979).
2. A. Modena, Z. Najmudln, A. E. Dangor, C. E. Clayton, K. A. Marsh, C.Joshi, V. Malka, C. B. Darrow, C. Danson, D. Neely and F. N. Walsh,”Electron acceleration from the breaking of relativistic plasmawaves,” Nature 337, 606 (1995).
3. D. Umstadter, S.-Y. Chen, A. Maksimchuk, G. Mourou, and R. Wagner,”Nonlinear optics in relativistic plasmas and laser wakefield acceleration of electrons,” Science 273, 472-475, (1996).
4. S. P. D. Mangles, C. D. Murphy, Z. Najmudin, A. G. R Thomas, J. L.Collier, A.E. Dangor, P. S. Foster, J. L. Collier, E. J. Divall, J. G.Gallacher, C. J. Hooker, D. A. Jaroszynski, A. J. Langley, W. B. Mori, P. A.Norreys, F. S. Tsung, R. Viskup, B. R. Walton and K. Krushelnick,”Mono-energetic relativistic electron beams from intense laser plasma interactions,” Nature 431, 535 (2004).
5. J. Faure, Y. Glinec, A. Pukhov, S. Kiselev, S. Gordienko, E. Lefebvre,J.-P. Rousseau, F. Burgy & V. Malka “A laser-plasma accelerator producing monoenergetic electron beams”, Nature 431,541 (2004).
6. C. G. R. Geddes, Cs. Toth, J. van Tilborg, E. Esarey, C. B. Schroeder, D.Bruhwiler, C. Nieter, J. Cary, W. P. Leemans “High-quality electron beams from a laser wakefield accelerator using plasma-channel guiding,” Nature 431, 538 (2004).
7. A. Maksimchuk, S. Reed, N. Naumova, V. Chvykov, B. Hou, G. Kalintchenko,T. Matsuoka, J. Nees, P. Rousseau, G. Mourou, and V. Yanovsky, “Energy scaling of quasi-monoenergetic electron beams from laser wakefields driven by 40 TW ultrashort pulses,” Appl. Phys. B: Lasers and Optics 89, 201 (2007).
8. A. Maksimchuk, S. Reed, S. S. Bulanov, V. Chvykov, G. Kalintchenko, T.Matsuoka, C. McGuffey, G. Mourou, N. Naumova, J. Nees, P. Rousseau, V.Yanovsky, K. Krushelnick, N. H. Matlis, S. Kalmykov, G. Shvets, M. C. Downer,C. R. Vane, J. R. Beene, D. Stracener, and D. R. Schultz, “Studies of laser wakefield structures and electron acceleration in underdense plasmas,” Phys. Plasmas 15, 056703 (2008).
9. S. A. Reed, V. Chvykov, G. Kalintchenko, T. Matsuoka, P. Rousseau, V.Yanovsky, C. R. Vane, J. R. Beene, D. Stracener, D. R. Schultz, and A.Maksimchuk, “Photonuclear fission with quasi-monoenergetic electron beams from laser wakefields,” Appl. Phys. Lett. 89, 231107-1-3 (2006).
10. S. A. Reed, V. Chvykov, G. Kalintchenko, T. Matsuoka, P. Rousseau, V.Yanovsky, C. R. Vane, J. R. Beene, D. Stracener, D. R. Schultz and A.Maksimchuk, “Efficient initiation of photonuclear reactions using quasimonoenergetic electron beams from laser wakefield acceleration,” Journal of Applied Physics 102, 073103 (2007).
11. N. H. Matlis, S. Reed, S. Bulanov, V. Chvykov, G. Kauntchenko, T.Matsuoka, P. Rousseau, V. Yanovsky, A. Maksimchuk, S. Kalmykov, G. Shvets, and M. C. Downer, Snapshots of laser wakefields, NaturePhysics 2, 749-53, (2006).
12. S. A. Reed, V. Chvykov, G. Kalintchenko, T. Matsuoka, P. Rousseau, V. Yanovsky, C. R. Vane, J. R. Beene, D. Stracener, D. R. Schultz, and A. Maksimchuk, “Photonuclear fission with quasi-monoenergetic electron beams from laser wakefields,” Appl. Phys. Lett. 89, 231107-1-3 (2006).
13. S. A. Reed, V. Chvykov, G. Kalintchenko, T. Matsuoka, P. Rousseau, V. Yanovsky, C. R. Vane, J. R. Beene, D. Stracener, D. R. Schultz and A. Maksimchuk, “Efficient initiation of photonuclear reactions using quasimonoenergetic electron beams from laser wakefield acceleration,” Journal of Applied Physics 102, 073103 (2007).
14. Z.-H. He, A. G. R. Thomas, B. Beaurepaire, J. A. Nees, B. Hou, V. Malka, K. Krushelnick, and J. Faure, “Electron diffraction using ultrafast electron bunches from a laser-wakefield accelerator at kHz repetition rate,” Appl. Phys. Lett. 102, 064104 (2013).