Experiments using the Omega EP Laser
In addition to the experiments performed on our in house facilities, we also run experimental campaigns on larger National Laboratory scale facilities when higher energies are required to make the measurements of interest and observe how phenomena scale with energy. Our group has recently been performing experiments on both the Omega EP laser facility at the Laboratory for Laser Energetics (LLE) and the Jupiter Laser Facility at the Lawrence Livermore National Laboratory (LLNL).
Omega EP laser
We have been performing experiments on the Omega EP laser facility, housed at the LLE, University of Rochester, since 2009, which is supported by the National Laser Users’ Facility program. Our studies have been investigating high-intensity interactions with low-density plasmas. The shot campaigns have focused on a range of plasma density regimes, studying particle acceleration from, and laser channeling through, both underdense plasma and near-critical density plasma.
The dual short-pulse beams available at the Omega EP facility are ideal for performing proton-probing experiments. The proton probing diagnostic uses a laser accelerated proton beam to observe the quasi-static electric and magnetic fields generated during the high-intensity laser interactions.
A UV long-pulse beam is used to create a plasma plume underdense plasma target. The main short-pulse interaction beam (750 J, 9 ps) is focused through the plume, creating a channel as it propagates through and accelerates electrons and ions. The second short-pulse was used to generate a proton beam and the channel formation was captured as the laser was in the plasma (figure 1). Filamentation of the laser creating several channels is followed by self-correction into a single channel as the interaction progresses [1,2]. These features are in excellent agreement with particle-in-cell simulations, such as in figure 2, which shows similar structure to the experiment.
![Figure 1: Proton probe images of the laser pulse propagating through the plasma from left to right. The time sequence is shown on the right hand side and shows channel wall modulations, filamentation and channel self-correction. Data published in [1,2].](https://cuos.engin.umich.edu/wp-content/uploads/sites/114/2025/01/Omega_1.jpg)
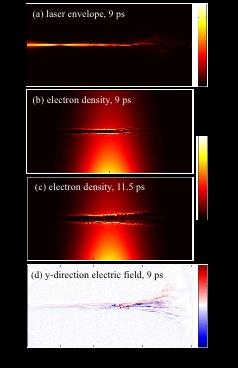
The near-critical plasma density regime it is difficult to explore with well-controlled experiments. Typical laser wavelengths of around 1 µm (the Omega EP short pulse beam has λ = 1.053 µm) give a critical plasma density of nc = 1 x 1021 cm-3. Easily implementable targets are either gas-jet targets, producing an underdense plasma ne = 1018 – 1020 cm-3, (0.001nc – 0.1nc), or solid density foils, producing an overdense plasma ne > 1023 cm-3 (> 100nc). A solid target has some position within the expanding plasma plume, which will be at critical density, but only over a very short scale length and is difficult to control. To bridge the gap in density, we use very low-density foam targets, which cover a density range from 0.9nc to 30nc.
At extreme intensities, which can now be achieved by state-of-the-art laser systems (up to 1022 Wm-2), the peak normalized vector potential a0 can exceed unity so that relativistic effects become important. The electrons oscillate within the laser fields at speed approaching the speed of light, altering their effective mass. This in turn modifies the plasma frequency, ωpe = (ne e2 / (ε0 <γ>me))1/2 , and therefore the critical density increases by the Lorentz factor <γ>. Relativistically induced transparency is when a classically over-critical plasma, ne > nc, becomes underdense, allowing the laser to propagate up to the relativistic critical density, nγc = <γ> nc. As the laser propagates into the plasma, the ponderomotive force of the tightly focused laser expels electrons from the regions of highest intensity, setting up a radial electric field. In respond to this field, the ions are accelerated transversely to leave behind a cavitated channel.
![Figure 3: Taken from [4]: (a) The simulation channel length for different densities (red), the hole boring model scaling, and model estimate for channel length. (b) The channel advancement speed from the simulation.](https://cuos.engin.umich.edu/wp-content/uploads/sites/114/2025/01/fig3_external-facilities-copy.jpg)
Our experiments and modeling have shown [3,4] that the relativistically induced transparency can lead to channel formation in plasmas of ne > nc, but ne < nγc at a rate much faster than the hole boring model [5] predicts (see figure 3). By performing a balance between the laser energy, EL and the energy that the electrons acquire, (assuming a mean energy), Epe, we found a general estimate for the generated channel length, d, in near-critical density plasmas [4].
In figure 3 the observed channel depth (and channeling speed) versus the different simulation plasma densities and this illustrates that the channel is deeper (and faster propagating) than predicted by the hole boring model. Our model is in good agreement with the simulation results, which is shown the dashed line labeled “model” in figure 3 (a).
The National Laser Users’ Facility (NLUF) supports our work on Omega EP through grant numbers DE-FF52-09NA29041 and DE-NA000874.
Titan laser
The Titan laser is part of the Jupiter Laser Facility (JLF) at the LLNL. We were awarded 4 weeks of experimental access time to study near-critical density plasma interactions during early 2012. In particular, the effect of target density on the temperature of the accelerated electrons and proton beam generation were investigated. The high-intensity short pulse beam can nominally provide 1 ps, 150 J or 10 ps, 300 J laser pulses focused to around intensities of around 5 x 1019 Wcm-2.
A strong correlation between plasma density and the accelerated electron momentum from the interaction has been observed in particle-in-cell simulations [4], as shown in figure 4. Laser-electron coupling is fundamental to the whole of a laser-plasma interaction so understanding the electron heating and energy transfer in this near-critical regime in central to many observed phenomena.
![Figure 4: Taken from [4]: (a) The longitudinal momentum spectra and (b) the transverse momentum spectra for the different density simulations. (c) pfit to the spectra against plasma density.](https://cuos.engin.umich.edu/wp-content/uploads/sites/114/2025/01/fig4_external-facilities-copy.jpg)
References:
[1] L. Willingale, et al., Physical Review Letters, 106, 105002 (2011)
[2] L. Willingale, et al., IEEE Transactions on Plasma Science, 39, 2616 (2011)
[3] L. Willingale, et al., Physical Review Letters, 102, 125002 (2009)
[4] L. Willingale, et al., Physics of Plasmas, 18, 056706 (2011)
[5] S. C. Wilks, et al., Physical Review Letters, 69, 1383 (1992)
 MENU
MENU