The Relativistic Lambda Cubed Regime
For centuries the microscope has carried the ability to concentrate light transversely to the limit of a single wavelength. It is only more recently, however, that the techniques to temporally concentrate light to approach a single period (or a single wavelength in the direction of propagation) have been developed. Bringing a small quantity of optical energy, say a millijoule of 800nm light, to an 800nm focal spot with a duration of a single cycle creates a focal intensity with intensity capable of driving relativistic motion in electrons. Similarly, the concentration of a few joules of light to such a small volume produces forces sufficient to produce relativistic motion in protons.
The intensity of a pulse of light at focus is nearly proportional to the pulse energy and inversely proportional to the pulse duration and the focal area. Take to the wavelength limit the intensity is inversely proportional to the cube of the wavelength, lambda cubed.
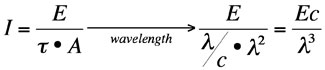
Taken in this limit one on the principle kernels of charged particle dynamics can be transformed, changing its wavelength dependence. While this does not alter the basic physics of the interactions, it does suggest that shorter wavelengths may have a more prominent role in some interactions.
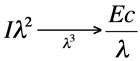
The energy required to drive electrons to relativistic energy and to open the portal to relativistic phenomena is actually lower for shorter wavelengths. Consequently, laser systems may be employed to explore the relativistic phenomena such as electron-positron pair generation, relativistic nonlinear optics, radiation reaction, and the like with some additional fundamental benefits:
• The concentration of light to a single wavelength subjects interactions driven at focus to a clean single-mode electromagnetic structure.
• Both spatial and temporal gradients surrounding the interaction region are maximized.
• High repetition rates are enabled because lower energy pulses reduce heat dissipation problems in laser design.
• Microscopic interactions can be extremely strong, leading to a kind of relativistic optoelectronics.
 MENU
MENU