Chirped Pulse Amplification
Remarkable progress in development of high power femtosecond pulses and their applications has been achieved since introduction of chirped pulse amplification (CPA) in mid 1980s. Peak laser power and focused intensity has increased several orders of magnitude. Electrons oscillating in the field of such intense light become relativistic. New fields of physics-relativistic optics and high-field science have been borne thus bridging optics, nuclear physics and plasma physics.
Increasing laser peak power and intensity has been one of the most important problems for laser science and technology since invention of a laser in early 1960s. Historically it has been addressed by developing methods to shorten pulse duration. Q-switching and mode-locking techniques, developed in 60s, pushed peak powers to MW and GW range and thus made possible discoveries of the basic nonlinear optics effects- harmonics generation, nonlinear Raman and Brillouin scattering, 4-wave mixing, self-focusing etc. The underlying reason enabling to open the realm of nonlinear optics was the fact that laser electric field became comparable to an intraatomic electric field. Therefore, a response of an atom to the applied laser field became dependent nonlinearly on laser intensity. Ironically, the same reason dramatically slowed down further progress in increasing laser peak power in 70’s and 80’s (Fig.1).

Nonlinear response of a material can be described by introducing a proportional to laser intensity I [W/cm2] additive to a refractive index at low intensity n0.
n=n0+n2I (1)
where n is index of refraction, n2 [cm2/W] – is a material dependent nonlinear index coefficient.
Remarkably, this simple formula describes vast majority effects in short pulse lasers. Phase of the laser electric field not only depends on intensity according to (1) but also parametrically depends on spatial coordinates and time through the dependence of I on space and time. The spatial dependence leads to intensity dependent focusing lens (Kerr-lens) for beams with larger intensity in the center (most common case) causing beam self-focusing. The temporal dependence causes generation of new frequencies through self-phase-modulation and together with the Kerr-lens provides the most effective modern short-pulse generation mechanism- Kerr-lens-mode-locking (KLM).
Solids are the most efficient laser materials but n2 in solids is high enough to cause catastrophic (leading to material damage) self-focusing of a laser beam at intensities in the GW/cm2 range. Efficient extraction of the energy stored in the laser active medium requires that output fluence should be of the order of the medium saturation fluence. Typically saturation fluence for solid state laser materials ranges between 1 and 10 J/cm2, therefore only pulses of nanosecond duration or longer could be efficiently amplified without damaging the laser. Although picosecond lasers were developed, the output fluence for those lasers had to be kept well below saturation fluence to avoid material damage caused by self-focusing. In femtosecond range of the pulsewidth, dye femtosecond lasers were developed but dyes have very low saturation fluence (mJ/cm2) which resulted in relatively low power. Self-focusing intensity limit kept high power solid state lasers bulky and expensive until introduction of CPA (by former CUOS director G. Mourou et al. [1,2]) in late 80s because increasing a beam size seemed to be the only way to increase the output power.
In CPA a short laser pulse is expanded to a nanosecond pulsewidth, amplified at intensities that are below the amplifier damage threshold and compressed in air or vacuum to a subpicosecond pulsewidth (Fig.2). Expansion and subsequent compression
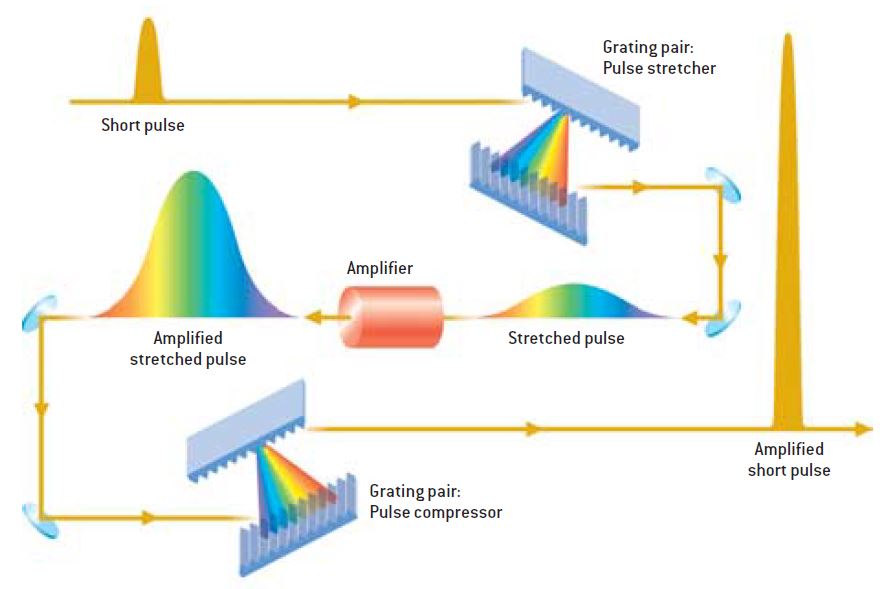
are provided by introduction of a frequency dependent delay in the pulse spectrum. An expanded pulse has its frequency changing with time and is called a “chirped” pulse. The term “chirped” came from radar technology where it was used earlier for similar pulse manipulation. A chirp is called positive if lower frequency light travels ahead of higher frequency light and negative if opposite holds. Typically, a device (called stretcher or expander) introduces positive chirp and thus provides for a long chirped pulse suitable for amplification. After amplification a negative chirp provided by a compressor compensates for the positive chirp introduced by a stretcher and a short pulse is restored. A pair of prism [3] or more typically a grating pair [4] serves as a compressor.
The first demonstrated CPA lasers [1] (they were based on Nd:glass) were somewhat more complicated because subpicosecond Nd:glass oscillators did not exist at the time. A combination of self-phase modulation and group velocity dispersion in optical fiber was used to expand the spectrum and to chirp the pulse of a picosecond oscillator. A chirp introduced by the fiber was not well matched to the chirp of the grating compressor leading to poor quality of the compression and low compression ratio. A breakthrough came after Martinez [5] realized that placing a 1:1 telescope inside the compressor changes the sign of the chirp introduced by the compressor. Mourou et al [2] made the first well-matched stretcher/compressor combination by making a grating stretcher with a telescope inside. Discovery of Kerr-lens-modelocking in early 90s [6] gave a significant boost to CPA lasers by making a stable femtosecond oscillator development possible and thus simplifying a CPA laser design.
While the most advanced CPA lasers are built on the basis of Ti:sapphire and Nd:glass, CPA has been demonstrated for the most broadband solid state materials: Cr: LISAF [7,8], Cr: forsterite [9], Yb:glass [10,11], Ce:LICAF [12] etc. A modern CPA laser consists of the following main parts: femtosecond oscillator, stretcher, amplifier, compressor and focusing system.
Ti: sapphire high peak power lasers
Ti:sapphire is almost an ideal material for CPA lasers. It exhibits excellent mechanical and thermal properties and the largest bandwidth of the laser transition -230 nm. The saturation fluence of Ti:sapphire (0.9 J/cm^2) allows efficient energy extraction at sub-nanosecond pulsewidth below damage threshold of dielectric coatings. The only problem with Ti: sapphire – relatively short lifetime of the upper laser level- 3 ms, makes laser pumping necessary. Frequency doubled Nd:YAG, Nd: YLF, and Nd: glass lasers are used to pump Ti: sapphire. High energy Nd:YAG lasers with output energy up to 4J at the wavelength 532 nm and 10 Hz repetition rate are commercially available. Larger energy can be extracted from Nd:glass lasers and used to pump Ti:sapphire at lower repetition rate or even on a single shot basis. Ultimate limitation of the output energy is imposed by the available crystal size. Currently, good optical quality crystals of up to ~10 cm diameter are commercially available (Crystal Systems). It means that up to 150 J can be potentially extracted in a single beam (assuming extraction at twice the saturation fluence value). The bandwidth is mainly limited by gain narrowing and can reach 40-50nm with shaping of the input spectrum. The gain flattening using spectrally selective elements like etalon or birefringent filter provide spectrum up to 80 nm and pulsewidth below 20fs.
Lasers with output powers of 50 TW and above at about 30 fs pulse pulsewidth and 10 Hz repetition rate are currently operational at several laboratories (University of Michigan (USA), LOA (France), JAERI (Japan), and MBI (Germany)). A 200 TW single shot laser (JANUSP) with longer pulsewidth (100 fs) is built in LLNL. A Petawatt [13] single shot laser is built at JAERI. Recently at the University of Michigan on HERCULES laser we achieved power of 300 TW in 30 fs at 0.1Hz repetition rate [14].
References:
1. D. Strickland and G. Mourou, “Compression of Amplified Chirped Optical Pulses,” Optics Comm. 56, 219 (1985).
2. M. Pessot, P. Maine and G, Mourou, “1000 Times Expansion/Compression of Optical Pulses for Chirped Pulse Amplification,” Optics Comm. 62, 419 (1987).
3. R. L. Fork, O. E. Martinez, and J. P. Gordon, “Negative Dispersion Using Pairs of Prisms,” Opt. Lett. 9, 150 (1984).
4. E. B. Treacy, “Optical Pulse Compression with Diffraction Gratings”, IEEE J. Quant. Electron. QE-5, 454 (1969).
5. O. E. Martinez, “3000 Times Grating Compressor with Positive Group Velocity Dispersion: Application to Fiber Compensation in 1.3-1.6 mm Region,” IEEE J. Quant. Electron. QE-23, 59 (1987).
6. D. E. Spence, P. N. Kean, and W. Sibbett, “60-fs Pulse Generation from a Self-Mode-Locked Ti:Sapphire Laser”, Opt. Lett. 16, 42 (1991).
7. T. Ditmire and M. Perry, Opt. Lett. “Terawatt Cr:LisrAlF6 Laser System,” 18, 426 (1993).
8. P. Beaud, M. Richardson, E. J. Miesak,”Multi-Terawatt Femtosecond Cr:LiSAF Laser,” IEEE J. of Quant. Electron. 31, 317 (1995).
9. G. Jonusauskas, J. Oberle, and C. Rulliere, “54-fs, 1GW, 1kHz Pulse Amplification in Cr:Forsterite,” Opt. Lett. 23, 1918 (1998).
10. C. Honninger, S. Biswal, A. Braun, C. Horvath, J. Nees, U. Keller, and G. Mourou, “Directly Diode-Pumped Yb:Glass Regenerative Chirped Pulse Amplifier,” in Conference on Lasers and Electrooptics, Vol. 6, of 1998 OSA Technical Digest Series (Optical Society of America, Washington, DC, 1998), paper CThJ4.
11. S. Biswal, J. Nees, A. Nishimura, H. Takuma, and G. Mourou, “Ytterbium-doped Glass Regenerative Chirped-pulse Amplifier,” Opt. Comm. 160, 92 (1999).
12. Z. Liu, T. Kozeki, Y. Suzuki, N. Sarukura, K. Shimamura, T. Fukuda, M. Hirano, and H. Hosono, “Chirped-pulse amplification of ultraviolet femtosecond pulses by use of Ce 3+ LiCaAlF 6 as a broadband, solid-state gain medium,” Opt. Lett. 26, 301 (2001).
13. M. D. Perry, D. Pennington, B. C. Stuart, G. Tiethbohl,, J. A. Britten, C. Brown, S. Hermann, B. Golick, M. Kartz, J. Miller, H. T. Powell, M. Vergino, and V. Yanovsky,” Petawatt Laser Pulses,” Opt. Lett. 24, 160 (1999).
14. V. Yanovsky, V. Chvykov, G. Kalinchenko, P. Rousseau, T. Planchon, T. Matsuoka, A. Maksimchuk, J. Nees, G. Cheriaux, G. Mourou and K. Krushelnick, “Ultra-high intensity 300 TW laser at 0.1 Hz repetition rate,” Optics Express 16, 2109 (2008).
 MENU
MENU